Logistic regression is a method for calculating probabilities for problems with limited (often two) potential outcomes. Unlike linear regression, it ensures values can never be greater than 1 or less than 0.
Before we discuss how it works: Why not just use linear regression?
Suppose you label a set of two possibilities (say, whether an email is spam) as “0” and “1”. With linear regression, you’d create a straight line that best tries to fit those two highly different outcomes. That usually isn’t ideal for a few reasons.
Firstly: the line can be extrapolated beyond the bounds of 0 and 1. For a binary outcome, this is impossible: you can’t have a 110% chance (or a -10% chance) that something will happen.
Similarly, linear regression doesn’t output probabilities, it just attempts to minimize the distance between points and the hyperplane.
By contrast, logistic regression creates an S-shaped curve that:
- Cannot have values greater than 1 or less than 0
- Can have its results interpreted as probabalistic outcomes
So what is logistic regression?
Logistic regression uses the sigmoid function, that is:
![\[y' = frac{1}{1 + e^{-z}}\]](https://www.shamefulblog.com/wp-content/ql-cache/quicklatex.com-22c10a490a1b56a33d0df99d39e81df6_l3.png "Rendered by QuickLaTeX.com")
to output a value between zero and 1. If z represents the output of the linear model, sigmoid(z) will yield a probability of a classification.
In the above:
- y’: Output of the logistic regression for an example
- z:
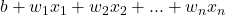–> that is, the output of the linear regression model
Conversely, z is often called the “log odds”, because the inverse of the sigmoid asserts z is the log of the probabilty of the “1” label divided by teh probability of the “0” label. That is:
![\[z = log(frac{y}{1-y})\]](https://www.shamefulblog.com/wp-content/ql-cache/quicklatex.com-6df1aeb652f65942969e11c0fc6e1886_l3.png "Rendered by QuickLaTeX.com")
technically you could have value outputs above 1 or below zero. This is obviously aburd: there is never, say, a 110% or -5% chance an email is spam – it has to be between 0-1.
Similarly, linear regression doesn’t output probabilities, it just attempts to minimize the distance between the points and the hyperplane – that hyperplane cannot be interpreted as probabilities.
In short: the problem is when we’re working with binary data, we don’t want a straight line to separate “0” and “1” examples, we’re more interested in the data that is almost certainly true, the data that is almost certainly false, a
By contrast, logistic regression attempts to squeeze the output
Logistic regression and loss functions
While linear regression uses squared loss as its loss function, logistic regression uses log loss. That is:
![\[Log Loss = sum_{(x,y)in D} -y log(y') - (1-y)log(1-y')\]](https://www.shamefulblog.com/wp-content/ql-cache/quicklatex.com-96b0f2d33188e6d8a6911576d9c52a42_l3.png "Rendered by QuickLaTeX.com")
Where:
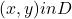: the data set- y: the label in a labeled example
- y’: The predicted value (somewhere between 0 and 1)
Regularizing Logistic Regregssion
Regularization is important in logistic regression modeling, otherwise data will become very overfit. Most logistic regression models either stop early, or use 
regularization.