Sparse vectors (that is, vectors where most values are zero) often have a lot of dimensions. When we create feature crosses for those vectors, we create even more dimensions. This can create enormous models that require large amounts of memory to process.
To save memory and reduce noise, we can zero-out features (that is, reduce their weights to zero). For situations where feature crosses include a lot of data that is likely to be zero (eg: if we cross latitude and longitude for the whole world into small areas, then determine which of those blocks are likely to have buffalo living in them, we can zero out any block that is entirely ocean). By dropping the weights to zero, we can prevent the need for storing them in memory.
We can do this by regularization, but ![]() regularization won’t do the job.
regularization won’t do the job. ![]() encourages small weights, but not truly zero.
encourages small weights, but not truly zero.
![]() regularization encourages unhelpful coefficients to be exactly zero.
regularization encourages unhelpful coefficients to be exactly zero.
How 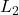 and
and 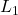 regularization differ
regularization differ
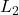 penalizes
penalizes 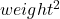 , whereas
, whereas 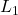 penalizes |weight|
penalizes |weight|- So while the derivative of
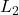 is 2 * weight, the derivative of
is 2 * weight, the derivative of 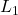 is “k” – a constant, entirely independent of weight.
is “k” – a constant, entirely independent of weight.
![]() works by substracting some constant value from every weight. Once a weight goes below 0, it will be set to 0.
works by substracting some constant value from every weight. Once a weight goes below 0, it will be set to 0.