Why Use Non-Linear Functions?
When working with basic nonlinear problems, we can use feature crosses to simplify the data. (Eg: if we have values with negative x & y and positive x & y with a similar trend, we can create a linear solution through the feature cross x * y).
For more difficult nonlinear problems (eg: a spiral or even more random shapes), trying to manually arrange the data into linear patterns becomes increasingly challenging. At some point, we likely want to employ non-linear functions to determine challenging associations.
We can pipe hidden layers (that is, layers that, for example, have been given weights) through to a non-linear transformation layer. These non-linear layers are called activation functions
Adding multiple levels of nonlinearities allows us to model far more complicated relationships.
Some examples of non-linear functions include:
- Rectified linear units or (ReLU):
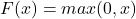
- An extremely simple nonlinear function, ReLUs eliminate any negative values and return zero instead.
- Sigmoid functions
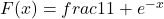
- Referenced earlier in logistic regression, sigmoid functions ensure all return values are between 0 and 1
TensorFlow provides many out-of-the-box activation functions.
So what are Neural Networks?
Neural networks are:
- A set of nodes, organized in layers
- A set of weights that represent connections between each layer and the layer beneath it
- A set of biases (one for each node)
- An activation function that transforms the output of each node in each layer